Giáo án Toán 7 (Cánh diều) - Chương 7: Tam giác - Bài 13: Tính chất ba đường cao của tam giác
I Đường cao của tam giác
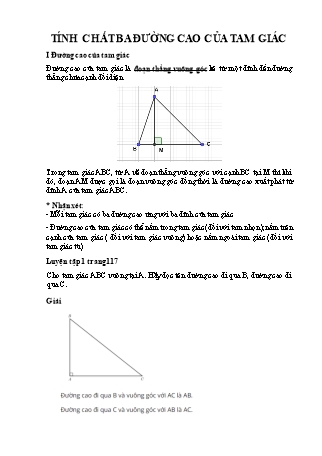
Đường cao của tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện
Trong tam giác ABC, từ A vẽ đoạn thẳng vuông góc với cạnh BC tại M thì khi đó, đoạn AM được gọi là đoạn vuông góc đồng thời là đường cao xuất phát từ đỉnh A của tam giác ABC.
* Nhận xét:
- Mỗi tam giác có ba đường cao ứng với ba đỉnh của tam giác
- Đường cao của tam giác có thể nằm trong tam giác (đối với tam nhọn); nằm trên cạnh của tam giác ( đối với tam giác vuông) hoặc nằm ngoài tam giác (đối với tam giác tù)
Luyện tập 1 trang 117
Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.
Bạn đang xem tài liệu "Giáo án Toán 7 (Cánh diều) - Chương 7: Tam giác - Bài 13: Tính chất ba đường cao của tam giác", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Giáo án Toán 7 (Cánh diều) - Chương 7: Tam giác - Bài 13: Tính chất ba đường cao của tam giác
TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC I Đường cao của tam giác Đường cao của tam giác là đoạn thẳng vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện Trong tam giác ABC, từ A vẽ đoạn thẳng vuông góc với cạnh BC tại M thì khi đó, đoạn AM được gọi là đoạn vuông góc đồng thời là đường cao xuất phát từ đỉnh A của tam giác ABC. * Nhận xét: - Mỗi tam giác có ba đường cao ứng với ba đỉnh của tam giác - Đường cao của tam giác có thể nằm trong tam giác (đối với tam nhọn); nằm trên cạnh của tam giác ( đối với tam giác vuông) hoặc nằm ngoài tam giác (đối với tam giác tù) Luyện tập 1 trang 117 Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C. Giải III Tính chất ba đường cao của tam giác Trong một tam giác, ba đường cao cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác. Từ đây ta, quy ước giao điểm của ba đường cao là điểm H và H được gọi là trực tâm của tam giác. Nhận xét: Để xác định trực tâm của một tam giác, ta chỉ cần vẽ hai đường cao bất kì và xác định giao điểm của hai đường đó. * Phương pháp xác định trực tâm đối với từng dạng tam giác TH1:Trực tâm trong tam giác nhọn B1: Vẽ tam giác nhọn ABC B2: Từ B hạ một đường vuông góc xuống cạnh AC tại E; Từ C hạ một đường vuông góc xuống cạnh AB tại F. Khi đó, hai đường cao BE và CF cắt nhau tại một điểm, ta đặt tên cho điểm đó là H và H là trực tâm của tam giác ABC. TH2:Trực tâm trong tam giác vuông B1: Vẽ tam ABC vuông tại A B2: Do tam giác ABC vuông tại A nên cạnh góc vuông BA và CA là hai đường cao của tam giác ABC. Lúc này, ta dùng thước kéo dài hai cạnh góc vuông BA và CA. Khi đó, hai đường thẳng này cắt nhau tại đỉnh A và đỉnh A lúc này được gọi là trực tâm của tam giác. Như vậy trong tam giác vuông thì trực tâm của tam giác trùng với đỉnh góc vuông. TH3: Trực tâm trong tam giác tù B1: Vẽ tam ABC tù tại A B2: Dùng thước kéo dài hai cạnh góc tù BA và CA. B3: Từ B hạ một đường vuông góc với CA tại E, Từ C hạ một đường vuông góc với BA tại F. Khi đó, hai đường BE và CF là hai đường cao của tam giác ABC. B4: Kéo dài hai đường BE và CF. Khi đó, hai đường thẳng BE và CF cắt nhau tại một điểm. ta đặt tên cho điểm này là H và điểm H được gọi là trực tâm của tam giác ABC Luyện tập 2 trang 117 Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC. Giải Phương pháp: Ta chứng minh G là giao điểm của hai đường cao BM và CN nghĩa là ta đi chứng minh BM và CN là hai đường cao của tam giác ABC Hướng làm Chứng minh nên (hai góc tương ứng bằng nhau) Mà (hai góc kề bù) Suy ra Suy ra BM vuông góc với AC tai M Nên BM là đường cao Chứng minh tương tự, ta cm được CN vuông góc với AB tại N Nên CN là đường cao Mà BM và CN cắt nhau tại G nên G là trực tâm của tam giác Luyện tập 3 trang 118 Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều. Giải Phương Pháp: Cách 1: CM 3 cạnh bằng nhau Cách 2: CM 3 góc bằng nhau Cách 3: CM tam giác đề cho là tam giác cân và có một góc bằng 600 . Ở đây, đề cho yếu tố đường trung tuyến nên ta chúng minh theo cách 1 Gọi M là giao điểm của BH và AC; N là giao điểm của CH và AB Vì H là trực tâm đồng thời là trọng tâm của tam giác ABC nên ta có: Xét tam giác vuông AMB và tam giác vuông CMB có BM là cạnh chung MA = MC ( BM là đường trung tuyến) Suy ra (hai cạnh góc vuông) Nên AB = CB (hai cạnh tương ứng) (1) CM tương tự, ta cm được (hai cạnh góc vuông) Nên AC = CB (hai cạnh tương ứng) (2) Từ (1) và (2) suy ra AB = CB = AC Vậy tam giác ABC đều.
File đính kèm:
 giao_an_toan_7_canh_dieu_chuong_7_tam_giac_bai_13_tinh_chat.docx
giao_an_toan_7_canh_dieu_chuong_7_tam_giac_bai_13_tinh_chat.docx

