Giáo án ôn tập Toán 8 (Cánh diều) - Chương 8, Bài 4: Tính chất đường phân giác của tam giác
A. KIẾN THỨC TRỌNG TÂM.
1. Định lí.
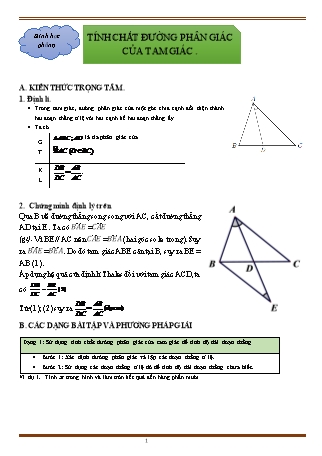
Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Ta có
GT là tia phân giác của
KL .
2. Chứng minh định lý trên.
Qua B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại E . Ta có (BAE) ̂ =(CAE) ̂
(gt). Vì BE // AC nên (CAE) ̂ =(BEA) ̂ (hai góc so le trong). Suy ra (BAE) ̂ =(BEA) ̂. Do đó tam giác ABE cân tại B, suy ra BE = AB (1).
Áp dụng hệ quả của định lí Thales đối với tam giác ACD, ta có
Từ (1); (2) suy ra
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Bạn đang xem tài liệu "Giáo án ôn tập Toán 8 (Cánh diều) - Chương 8, Bài 4: Tính chất đường phân giác của tam giác", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Giáo án ôn tập Toán 8 (Cánh diều) - Chương 8, Bài 4: Tính chất đường phân giác của tam giác
TÍNH CHẤT ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC . Hình học phẳng A. KIẾN THỨC TRỌNG TÂM. 1. Định lí. Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy. Ta có GT là tia phân giác của KL . 2. Chứng minh định lý trên. Qua B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại E . Ta có BAE =CAE (gt). Vì BE // AC nên CAE =BEA (hai góc so le trong). Suy ra BAE =BEA. Do đó tam giác ABE cân tại B, suy ra BE = AB (1). Áp dụng hệ quả của định lí Thales đối với tam giác ACD, ta có Từ (1); (2) suy ra B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI Dạng 1: Sử dụng tính chất đường phân giác của tam giác để tính độ dài đoạn thẳng Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ. Bước 2: Sử dụng các đoạn thẳng tỉ lệ đó để tính độ dài đoạn thẳng chưa biết. Ví dụ 1. Tính trong hình và làm tròn kết quả đến hàng phần mười. a) b) Lời giải Hình a: Do là đường phân giác trong của góc nên ta có Thay số ta có . Khi đó . Hình b: Với và do là đường phân giác trong của góc nên theo tính chất đường phân giác ta có Theo tính chất đường phân giác ta có . Dạng 2: Sử dụng tính chất đường phân giác của tam giác để tính tỉ số, chững minh các hệ thức, các đoạn thẳng bằng nhau, các đường thẳng song song Bước 1: Xác định đường phân giác và lập các đoạn thẳng tỉ lệ. Bước 2: Sử dụng các tỉ số đã có, cùng với các tính chất của tỉ lệ thức, các tỉ số trung gian (nến cần) và định lí đảo của định lí Ta-lét để tính tỉ số đoạn thẳng hoặc chứng minh các hệ thức. Từ đó suy ra các đoạn thẳng bằng nhau hay các đường thẳng song song. Ví dụ 2. Cho tam giác cân , có , . Đường phân giác của góc cắt tại , đường phân giác góc cắt tại . a) Chứng minh . b) Tính theo , . ĐS: . Lời giải a) Theo tính chất đường phân giác trong của góc và góc ta có ; (1) . (2) Từ và suy ra . Theo định lý Thales đảo ta được . b) Tính theo , . Theo có Do nên . Ví dụ 3. Cho tam giác có cm, cm, cm. Đường phân giác góc cắt tại . Qua kẻ (). a) Tính độ dài các đoạn thẳng , và . ĐS: ; ; . b) Cho biết diện tích tam giác là . Tính diện tích các tam giác , , theo . ĐS: ,,. Lời giải a) Theo tính chất đường phân giác trong góc ta có ; (1) Mặt khác . (2) Từ và ta tính được cm và cm. Vì nên ta có cm. b) Gọi là đường cao kẻ từ của . Ta có ; và . Suy ra và . Chứng minh tương tự bằng cách trong ta kẻ đường cao ta được ; và . Suy ra . và . C. BÀI TẬP VẬN DỤNG Bài 1. Cho tam giác vuông tại . Kẻ phân giác trong của (với ), biết cm, cm. Tính độ dài các đoạn thẳng , . ĐS: cm; cm. Lời giải Theo tính chất đường phân giác ta có . (1) Mặt khác, tam giác vuông tại nên theo định lý Py-ta-go ta có . (2) Từ và ta có hệ Bài 2. Cho tam giác , trung tuyến . Phân giác của cắt ở , phân giác của cắt ở . a) Chứng minh song song với . b) Gọi là giao điểm của và . Chứng minh là trung điểm của . Lời giải a) Theo tính chất đường phân giác ta có và . Mặt khác nên . Theo định lý Ta-lét đảo ta được . b) Theo câu a) ta có nên . Xét định lý Ta-lét cho và ta có và . Từ đó, suy ra mà nên hay là trung điểm của . Bài 3. Cho tam giác vuông tại và cm, cm. Đường phân giác góc cắt tại . a) Tính , và . ĐS: cm; cm; cm. b) Vẽ đường cao . Tính , và . ĐS: cm, cm, cm. Lời giải a) Áp dụng định lý Py-ta-go ta có Theo tính chất đường phân giác trong của góc ta có . Mặt khác ta lại có cm. Do đó cm. b) Ta có cm. Mặt khác cm. Áp dụng định lý Py-ta-go cho tam giác vuông ta có cm. Suy ra cm. Áp dụng định lý Py-ta-go cho tam giác vuông ta có cm. Bài 4. Cho tam giác cân (), đường phân giác góc cắt tại và cho biết cm, cm. a) Tính , . ĐS: cm; cm. b) Đường vuông góc với tại cắt đường thẳng kéo dài tại . Tính . ĐS: cm. Lời giải a) Ta có cm. (1) và . (2) Từ (1) và (2) suy ra . Từ đó suy ra cm, cm. b) Vì nên là phân giác ngoài của góc của tam giác . Khi đó ta có . Suy ra . Suy ra hay . Do đó cm. D. BÀI TẬP VỀ NHÀ Bài 5. Tính trong hình và làm tròn kết quả đến chữ số thập phân thứ nhất. a) b) Lời giải Hình a: Ta có . Theo tính chất đường phân giác trong ta có . Hình b: Ta có . Theo tính chất phân giác trong ta có . Bài 6. Cho tam giác , trung tuyến . Tia phân giác góc cắt tại , tia phân giác góc cắt cạnh tại . Chứng minh . Lời giải Theo tính chất đường phân giác ta có và . Mặt khác nên . Theo định lý Ta-lét đảo ta được . Bài 7. Cho tam giác có cm, cm, cm. Đường phân giác góc cắt tại . a) Tính độ dài các đoạn thẳng , . ĐS: cm; cm. b) Tính tỉ số diện tích hai tam giác và . ĐS: . Lời giải a) Áp dụng tính chất đường phân giác trong góc . Ta có ; (1) Mặt khác . (2) Từ và ta có tính được cm và cm. b) Gọi là đường cao kẻ từ của và là diện tích . Ta có ; và . Suy ra và . Do đó .
File đính kèm:
 giao_an_on_tap_toan_8_canh_dieu_chuong_8_bai_4_tinh_chat_duo.docx
giao_an_on_tap_toan_8_canh_dieu_chuong_8_bai_4_tinh_chat_duo.docx

