Giáo án ôn tập Hình học 7 (Kết nối tri thức với cuộc sống) - Chuyên đề: Tổng các góc trong một tam giác
I. LÍ THUYẾT TRỌNG TÂM
1. Định lí tổng ba góc của một tam giác
Tổng ba góc của một tam giác bằng 180o.
có
2. Áp dụng vào tam giác vuông
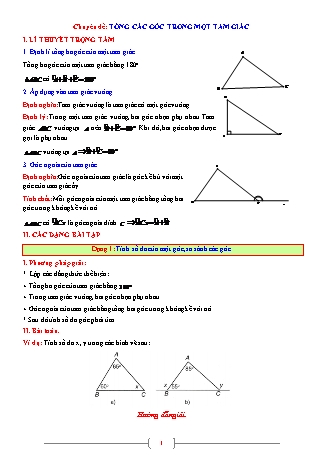
Định nghĩa: Tam giác vuông là tam giác có một góc vuông.
Định lý: Trong một tam giác vuông, hai góc nhọn phụ nhau. Tam giác vuông tại nên . Khi đó, hai góc nhọn được gọi là phụ nhau.
vuông tại
3. Góc ngoài của tam giác
Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác ấy.
Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.
có là góc ngoài đỉnh
Bạn đang xem 20 trang mẫu của tài liệu "Giáo án ôn tập Hình học 7 (Kết nối tri thức với cuộc sống) - Chuyên đề: Tổng các góc trong một tam giác", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Giáo án ôn tập Hình học 7 (Kết nối tri thức với cuộc sống) - Chuyên đề: Tổng các góc trong một tam giác
Chuyên đề: TỔNG CÁC GÓC TRONG MỘT TAM GIÁC I. LÍ THUYẾT TRỌNG TÂM 1. Định lí tổng ba góc của một tam giác Tổng ba góc của một tam giác bằng 180o. có 2. Áp dụng vào tam giác vuông Định nghĩa: Tam giác vuông là tam giác có một góc vuông. Định lý: Trong một tam giác vuông, hai góc nhọn phụ nhau. Tam giác vuông tại nên . Khi đó, hai góc nhọn được gọi là phụ nhau. vuông tại 3. Góc ngoài của tam giác Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác ấy. Tính chất: Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó. có là góc ngoài đỉnh II. CÁC DẠNG BÀI TẬP Dạng 1: Tính số đo của một góc, so sánh các góc I. Phương pháp giải: * Lập các đẳng thức thể hiện: + Tổng ba góc của tam giác bằng . + Trong tam giác vuông, hai góc nhọn phụ nhau.ID 05 072022 CDCB 7 STT55 + Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó. * Sau đó tính số đo góc phải tìm. II. Bài toán. Ví dụ: Tính số đo x, y trong các hình vẽ sau: Hướng dẫn giải a) Xét có b) Xét ∆ABC có y là góc ngoài tại đỉnh C. Suy ra . Lại có (hai góc kề bù). Suy ra . Bài 1: Cho tam giác ABC có và . a) Tính số đo các góc B, C của ∆ABC. b) Gọi AD là tia phân giác của . Tính số đo của . Lời giải a) Xét ∆ABC có . Theo giả thiết nên . Mặt khác (giả thiết). Suy ra: . . b) Do AD là tia phân giác góc nên . Xét ∆ACD có là góc ngoài đỉnh D nên . Bài 2: Cho ∆ABC có . a) Tam giác ABC là tam giác gì? b) Gọi AD là tia nằm giữa hai tia AB và AC . Biết . Tính số đo của . Lời giải a) Xét ∆ABC có . Do nên tam giác ABC là tam giác có một góc tù. b) Theo giả thiết, ta có . Xét ∆ADB có là góc ngoài đỉnh D nên . Bài 3: Tam giác ABC có số đo . Góc C có số đo bằng A. . B. . C. . D. . Lời giải Xét ∆ABC có . Bài 4: Cho tam giác ABC vuông tại B. Kết luận nào sau đây là sai? A. . B. . C. . D. . Lời giải Vì tam giác ABC vuông tại B nên (A đúng); (B và D đúng). C. sai vì nên . Bài 5: Cho tam giác MNP có . Biết . Số đo của bằng A. . B. . C. . D. . Lời giải Xét ∆MNP có . Mặt khác . Suy ra . Bài 6: Kết luận nào sau đây là đúng? A. Một tam giác chỉ có tối đa hai góc nhọn. B. Một tam giác chỉ có nhiều nhất một góc tù. C. Trong một tam giác, có ít nhất hai góc có số đo nhỏ hơn 60°. D. Trong một tam giác, số đo của mỗi góc luôn nhỏ hơn tổng số đo các góc còn lại. Lời giải A. Sai vì luôn tồn tại tam giác có ba góc nhọn. Ví dụ tam giác có ba góc bằng 60°. B. Đúng. Giả sử tam giác có nhiều hơn 1 góc tù. Khi đó tổng ba góc trong tam giác lớn hơn 180° (mâu thuẫn với định lí tổng 3 góc trong tam giác).Vậy trong tam giác có nhiều nhất một góc tù. C. Sai. Thật vậy xét tam giác ABC có . Khi đó (mâu thuẫn với định lí tổng 3 góc trong tam giác). D. Sai. Thậy vậy, xét ∆ABC có tù. Khi đó góc ngoài tại A là góc nhọn. Ta có (mâu thuẫn vì góc tù luôn lớn hơn góc nhọn). Bài 7: Cho tam giác ABC có và . Số đo của góc C bằng A. . B. . C. . D. . Lời giải ∆ABC có . Mặt khác nên . Bài 8: Cho tam giác ABC có . Biết góc B có số đo lớn hơn số đo góc C là 15o. a) Tính số đo các góc B và C của tam giác ABC. b) Gọi BD là tia phân giác của với . Tính số đo của . Lời giải a) Xét ∆ABC có . Mà (giả thiết) nên . b) Do BD là tia phân giác góc ABC nên . Xét ∆BCD có là góc ngoài đỉnh D nên . Bài 9: Cho tam giác ABC có AD, BE lần lượt là tia phân giác trong các góc Biết AD cắt BE tại K và . Tính số đo các góc A, B, C của tam giác ABC. Lời giải Ta có Do AK là phân giác của nên và . Xét ∆ABK có Mà BK là phân giác của nên . Xét ∆ABC có . Vậy ∆ABC có . Bài 10: Cho tam giác ABC. Tính số đo các góc còn lại của tam giác biết A. và . B. . C. và Lời giải Xét ∆ABC có . a) Có nên . b) Theo giả thiết . Áp dụng tính chất dãy tỉ số bằng nhau, ta có: Suy ra . c) Do nên ta có . Từ giả thiết . Áp dụng tính chất dãy tỉ số bằng nhau, ta có: Suy ra . Bài 11: Tính số đo trong hình vẽ dưới đây Lời giải Hình 1: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Hình 2: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Bài 12: Tính số đo trong hình vẽ dưới đây Lời giải Cách 1: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Cách 2: Ta có (trong tam giác vuông hai góc nhọn phụ nhau) . Vậy Bài 13: Tính số đo trong hình vẽ dưới đây Lời giải Ta có: (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) . Vậy Bài 14: Tính số đo trong hình vẽ dưới đây Lời giải Hình 1: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Hình 2: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Hình 3: Ta có: (hai góc kề bù) . Vậy Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Bài 15: Tính số đo trong hình vẽ sau: Biết và Lời giải Hình 1 Xét có (tính chất tam giác vuông) Ta lại có . Trong ta có . Mà . Hình 2 Ta có (hai góc kề bù). Xét có: (định lý tổng ba góc trong một tam giác) Ta lại có (góc ngoài của tam giác). Bài 16: Cho hình vẽ. Chứng minh rằng: Lời giải Xét có (tính chất tam giác vuông) Xét có . (tính chất tam giác vuông) Lại có Mặt khác Hay Bài 17: Tính các góc của , biết: và Lời giải Xét có . Mà Lại có: Bài 18: Tính các góc của tam giác biết: a) . b) . Lời giải a) . Ta có . Mà . b) . Ta có Mà . Bài 19: Cho tam giác , tia phân giác của góc cắt tại . Tính góc biết . Lời giải Ta có (định lý tổng 3 góc của một tam giác) Vì là tia phân giác của góc nên . Ta lại có (định lý tổng 3 góc của một tam giác) . Bài 20: Cho . Tính các góc của tam giác biết a) . b) . Lời giải a) Áp dụng định lí tổng 3 góc trong một tam giác ta có:ID 05 072022 CDCB 7 STT55 Áp dụng tính chất của dãy tỉ số bằng nhau ta được: . b) Ta có Áp dụng định lí tổng 3 góc trong một tam giác ta có: Bài 21: Cho biết . a) Tính các góc của tam giác . b) Tia phân giác ngoài tại cắt tại . Tính . Lời giải a) Từ suy ra: mà ( tổng 3 góc trong một tam giác) Áp dụng tính chất của dãy tỉ số bằng nhau ta được: . b) Ta có (mà là phân giác ngoài tại nên ) Ta có BÀI TẬP TỰ LUYỆN Bài 1: Tính số đo trong hình vẽ dưới đây Lời giải Xét H1: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Xét H2: Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Bài 2: Tính số đo trong hình vẽ dưới đây Lời giải Hình 1: Ta có: (hai góc kề bù) . Vậy Ta có: (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) . Vậy Hình 2: Ta có: (góc ngoài của tam giác bằng tổng hai góc trong không kề với nó) . Vậy Ta có: (định lý tổng ba góc trong một tam giác) . Vậy Bài 3: Cho . Tính các góc của tam giác biết a) . b) Lời giải a) , áp dụng tính chất của dãy tỉ số bằng nhau ta được: - Xét , áp dụng định lý tổng 3 góc trong một tam giác ta được : b) - Xét , áp dụng định lý tổng 3 góc trong một tam giác ta được: Ta có: , áp dụng tính chất của dãy tỉ số bằng nhau ta được: Bài 4: Cho tam giác có góc ngoài tại đỉnh có số đo bằng và . a) Tính các góc . b) Hai tia phân giác của góc và cắt nhau tại . Tính góc . Lời giải a) Tính các góc . Ta có góc ngoài tại đỉnh có số đo bằng nên . Ta lại có . Mà . b) Hai tia phân giác của góc và cắt nhau tại . Tính góc . Do tia là tia phân giác của góc Do tia là tia phân giác của góc . Ta lại có . Dạng 2: Các bài toán chứng minh góc Phương pháp giải: Sử dụng linh hoạt các tính chất về góc của một tam giác, góc ngoài tại một đỉnh hay tính chất tia phân giác của góc Bước 1. Áp dụng tính chất tổng ba góc trong tam giác, tính góc trong yêu cầu của bài toán. Bước 2. Kết hợp tính chất đường phân giác để chứng minh hệ thức. Ví dụ: Cho tam giác MNP. Các đường phân giác trong các góc M, P cắt nhau tại I. Chứng minh rằng: Hướng dẫn giải Xét ∆MIP có Lại có: (do MI là phân giác của ). (do PI là phân giác của ). Suy ra . (1) Mặt khác, xét ∆MNP có (2) Thế (2) vào (1), ta được (điều phải chứng minh) Bài 1: Cho tam giác ABC vuông tại A và . a) Chứng minh . b) Tia phân giác của cắt CH tại K. Chứng minh Lời giải a) Xét ∆ABC có . Xét ∆ABH có . Suy ra (điều phải chứng minh). b) Ta có AK là tia phân giác của nên . Mà (chứng minh câu a) nên suy ra (1). Mặt khác là góc ngoài đỉnh K của ∆AKC nên hay (2) Từ (1) và (2) ta có (điều phải chứng minh) Bài 2: Cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC . Các tia phân giác góc ABC và góc HAC cắt nhau tại I. Chứng minh rằng . Lời giải Xét ∆ABC vuông tại A có . (1) Xét ∆AHC vuông tại H có . (2) Từ (1) và (2), ta có . Lại có (do BI là phân giác của ); (do AI là phân giác của Suy ra (do ). Xét ∆ABI có: . Mà . Suy ra (điều phải chứng minh). Bài 3: Cho tam giác ABC có BD , CE lần lượt là tia phân giác các góc B, C. Gọi I là giao điểm của BD và CE. a) Chứng minh rằng . b) Biết . Tính số đo của . c) Tính số đo của biết số đo góc là trung bình cộng của hai góc . Lời giải a) Ta có (do BI là tia phân giác ), (do CI là tia phân giác ). Xét ∆IBC có . Suy ra (1) Xét ∆ABC có (2) Thế (2) vào (1) ta có: (điều phải chứng minh). b) Từ chứng minh câu a, ta có: . Mà ta có (hai góc kề bù). Suy ra . c) Do có số đo là trung bình cộng số đo của và nên hay Mà nên . Áp dụng chứng minh ở ý a ta có: . Bài 4: Cho tam giác ABC và đường cao AH . Biết rằng . a) Chứng minh rằng tam giác ABC là tam giác vuông. b) Biết rằng số đo góc bằng trung bình cộng của hai góc . Tính số đo các góc của tam giác ABC. Lời giải a) Xét ∆AHC vuông tại H có (1) Theo giả thiết, ta có hya Theo (1), ta có: . Vậy tam giác ABC vuông tại A. b) Do số đo góc bằng trung bình cộng của hai góc , nên ta có . (2) Tam giác ABC vuông tại A nên . (3) Từ (2) và (3) ta có: . Giải phương trình ta tìm được . Khi đó, ta có . Vậy ∆ABC có . Bài 5: Cho có . Kẻ vuông góc với (). Kẻ vuông góc với . Gọi là giao điểm của và . Chứng minh: . Lời giải Trong vuông tại , ta có: (hai góc phụ nhau) (1) Trong vuông tại , ta có: (hai góc phụ nhau) (2) Cộng (1) với (2) vế theo vế, ta có: Suy ra Bài 6: Cho góc , điểm thuộc tia . Kẻ vuông góc với (), kẻ vuông góc với (), kẻ vuông góc với (). Chứng minh: và . Lời giải + Ta có: (cùng phụ với ) + Ta có: (gt) Suy ra Suy ra (đồng vị) Bài 7: Cho vuông tại. Vẽ vuông góc với tại . Vẽ là tia đối của tia. Chứng minh: 1. 2. và bù nhau Lời giải 1. Xét , ta có Xét , ta có Mà nên . 2. Tương tự câu a, ta có Mà kề bù với nên bù với Bài 8: Cho vuông tại , điểm nằm trong tam giác đó. Chứng minh là góc tù. Lời giải Gọi là giao điểm của và Xét ta có: Xét ta có: Từ suy ra: là góc tù. Bài 9: Cho tam giác có .Vẽ phân giác . a) Chứng minh b) Đường thẳng chứa tia phân giác góc ngoài đỉnh của tam giác , cắt đường thẳng tại . Chứng minh rằng: Lời giải a) Sử dụng tính chất góc ngoài. Ta được: b) Ta có Mà . Từ đó suy Bài 10: Cho tam giác vuông tại . Gọi là đường thẳng vuông góc với tại . Tia phân giác của góc cắt ở và cắt d ở . Chứng minh rằng Lời giải Ta có: Suy ra . Bài 11: Cho tam giác vuông tại . Kẻ vuông góc với tại . Các tia phân giác của và cắt nhau tại . Chứng minh rằng . Lời giải Ta có , lần lượt là tia phân giác của và Nên và Mà (cùng phụ với ) nên Xét tam giác có: (định lý tổng 3 góc của một tam giác) . Bài 12: Chứng minh rằng: Tổng ba góc ngoài ở ba đỉnh của một tam giác bằng . Lời giải Giả sử : Xét , cần chứng minh Ta có: Cộng vế theo vế ta có Mà Cách khác: Dựa vào tính chất góc ngoài tam giác, tính số đo từng góc ngoài và thực hiện tương tự. Bài 13: Tam giác ABC có . Tia phân giác cắt BC tại D. a) Chứng minh . b) Đường thẳng chứa tia phân giác góc ngoài ở đỉnh A của tam giác ABC cắt đường thẳng BC tại E. Chứng minh rằng . Lời giải a) có ; có ; Mà nên . b) có (góc ngoài tam giác) có: (góc ngoài) hay . Bài 14: Cho tam giác ABC, O là điểm nằm trong tam giác. a) Chứng minh rằng . b) Biết và tia BO là tia phân giác của góc B. Chứng minh rằng tia CO là tia phân giác của góc C. Lời giải a) có (góc ngoài tam giác). có (góc ngoài tam giác). Hay. b) Từ mà BO là tia phân giác của nên suy ra Hay CO là tia phân giác của góc . BÀI TẬP TỰ LUYỆN Bài 1: Cho hình vẽ dưới đây. Chứng minh biết rằng: Lời giải Ta có: là góc ngoài của Hai góc trong cùng phía có tổng bằng Bài 2: Cho hình vẽ sau. Chứng minh rằng: Lời giải có ; có (cùng phụ ) Bài 3: Cho tam giác có . Gọi là đường thẳng đi qua và vuông góc với . Tia phân giác của góc cắt ở và cắt ở . Kẻ vuông góc với . Chứng minh rằng là tia phân giác của góc . Lời giải Ta có: ; mà CMTT Mà là phân giác của . Bài 4: Cho tam giác có , gọi là một điểm nằm giữa và . Lấy điểm thuộc tia đối của tia . Chứng minh rằng góc là góc nhọn. Lời giải Chứng minh ( tính chất góc ngoài của tam giác) .
File đính kèm:
 giao_an_on_tap_hinh_hoc_7_canh_dieu_chuyen_de_tong_cac_goc_t.docx
giao_an_on_tap_hinh_hoc_7_canh_dieu_chuyen_de_tong_cac_goc_t.docx

