Giáo án Hình học 6 (Cánh diều) - Chuyên đề 4.2: Hình bình hành, hình thoi

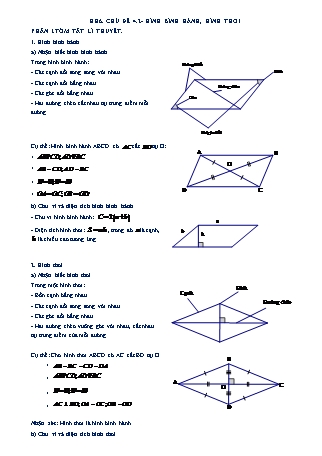
HH6. CHỦ ĐỀ 4.2- HÌNH BÌNH HÀNH, HÌNH THOI
PHẦN I.TÓM TẮT LÍ THUYẾT.
1. Hình bình hành
a) Nhận biết hình bình hành
Trong hình bình hành:
- Các cạnh đối song song với nhau.
- Các cạnh đối bằng nhau.
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm mỗi đường.
Cụ thể: Hình bình hành ABCD có cắt tại O:
+ 
+ 
+ 
+ 
b) Chu vi và diện tích hình bình hành
- Chu vi hình bình hành: 
- Diện tích hình thoi: , trong đó là cạnh, là chiều cao tương ứng.
2. Hình thoi
a) Nhận biết hình thoi
Trong một hình thoi:
- Bốn cạnh bằng nhau.
- Các cạnh đối song song với nhau.
- Các góc đối bằng nhau.
- Hai đường chéo vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường.
Cụ thể: Cho hình thoi ABCD có AC cắt BD tại O
	+ 
	+ 
	+ 
	+ 
Nhận xét: Hình thoi là hình bình hành.
b) Chu vi và diện tích hình thoi
- Chu vi hình thoi: 
- Diện tích hình thoi: , trong đó là độ dài hai đường chéo.
PHẦN II.CÁC DẠNG BÀI.
A. Hình bình hành
Dạng 1. Nhận biết hình bình hành
I.Phương pháp giải.
Các dấu hiệu nhận biết hình bình hành:
	1. Tứ giác có các cạnh đối song song là hình bình hành.
	2. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
	3. Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành.
	4. Tứ giác có các góc đối bằng nhau là hình bình hành.
	5. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
II.Bài toán.
Bài 1. Các tứ giác ở hình vẽ bên dưới có là hình bình hành không? Vì sao?
Lời giải
Cả ba tứ giác là hình bình hành
- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)
Chú ý:
- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.
- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.
Dạng 2. Cách vẽ hình bình hành	
I.Phương pháp giải.
Dựa vào các tính chất của hình bình hành để vẽ hình bình hành.
II. Bài toán.
Bài 1. Vẽ hình bình hành có ,. 
Lời giải 
Bước 1. Vẽ đoạn thẳng 
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho 
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.
Bài 2.Cho trước hai đoạn thẳng AB và CD như hình vẽ. Vẽ hình bình hành ABCD nhận AB và CD làm cạnh.
Lời giải 
Bước 1. 
- Vẽ một phần đường tròn tâm B bán kính AC.
- Vẽ một phần đường tròn tâm C bán kính AB.
Hai đườngtròn này cắt nhau tại D.
Bước 2. Nối D với B, D với C, ta được hình bình hành ABCD.
Bài 3. Vẽ hình bình hành có độ dài một cạnh bằng , một cạnh bằng .
Lời giải 
Bước 1. Vẽ đoạn thẳng 
Bước 2. Vẽ đường thẳng đi qua . Trên đường thẳng đó lấy điểm sao cho 
Bước 3. Vẽ đường thẳng đi qua và song song với , đường thẳng qua và song song với . Hai đường thẳng này cắt nhau tại , ta được hình bình hành .
Dạng 3. Tính chu vi và diện tích hình bình hành
I.Phương pháp giải.
	Dựa vào công thức tính chu vi và diện tích hình bình hành; mối quan hệ giữa các cạnh của hình bình hành.
II.Bài toán.
Bài 1. Cho hình bình hành có cạnh đáy là bằng và cạnh bên bằng và có chiều cao là . Hãy tính chu vi và diện tích hình bình hành đó.
Lời giải
Chu vi của hình bình hành là: 
Diện tích hình bình hành là: 
Bài 2. Cho hình bình hành có chu vi là , độ dài cạnh đáy bằng 5 lần cạnh kia, bằng 8 lần chiều cao. Tính diện tích của hình bình hành.
Lời giải
Gọi cạnh bên , ta có: cạnh đáy , chiều cao 
Chu vi hình bình hành = (cạnh bên + cạnh đáy) x 2 = 384
suy ra hay 
Do đó, cạnh bên , cạnh đáy , chiều cao 
Vì thế, diện tích hình bình hành là 
Bài 3. Một mảnh đất hình bình hành, biết cạnh đáy bằng , mở rộng mảnh đất bằng việc tăng cạnh đáy mảnh đất này thêm thì được mảnh đất hình bình hành mới có diện tích lớn hơn mảnh đất ban đầu là . Tính diện tích mảnh đất hình bình hành ban đầu.
Lời giải
Dựa vào công thức tính diện tích hình bình hành:
- Theo đầu bài, diện tích mảnh đất hình hành mới bằng .
- Do đó, chiều cao của mảnh đất là .
- Vì thế diện tích mảnh đất hình bình hành ban đầu là .
Bài 4. Một mảnh đất hình bình hành có cạnh đáy là . Người ta thu hẹp lại mảnh đất do bằng việc cắt giảm đáy của hình bình hành này khoảng nên hình bình hành mới có diện tích nhỏ hơn mảnh đất ban đầu là . Tính diện tích mảnh đất hình bình hành ban đầu.
Lời giải
Theo đầu bài, diện tích mảnh đất hình thoi bị cắt đi là .
 Do đó, chiều cao của mảnh đất là .
Vì thế, diện tích của mảnh đất hình bình hành ban đầu là . 
Bài 5. Mảnh đất hình bình hành có cạnh đáy là , mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là . hãy tính diện tích mảnh đất ban đầu.
Lời giải
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: 
Diện tích mảnh đất hình bình hành ban đầu là: 
Bài 6. Cho hình bình hành có chu vi là , có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Lời giải
Ta có nửa chu vi hình bình hành là: 
Nếu như coi cạnh kia là 1 phần thì cạnh đáy chính là 5 phần như vậy.
Ta có cạnh đáy hình bình hành là: 
Tính được chiều cao của hình bình hành là: 
Diện tích của hình bình hành là: 
Bài 7. Cho hình bình hành có chu vi là và độ dài cạnh đáy gấp 6 lần cạnh kia; gấp 2 lần chiều cao. Hãy tính diện tích hình bình hành đó
Lời giải
Nửa chu vi hình bình hành là: 
Cạnh đáy gấp 6 lần cạnh kia nên nửa chu vi sẽ gấp 7 lần cạnh kia.
Cạnh đáy hình bình hành là: 
Chiều cao hình bình hành là: 
Diện tích hình bình hành là: 
Bài 8. Một hình bình hành có cạnh đáy là . Người ta thu hẹp hình bình hành đó bằng cách giảm các cạnh đáy của hình bình hành đi được hình bình hành mới có diện tích nhỏ hơn diện tích hình bình hành ban đầu là . Tính diện tích hình bình hành ban đầu.
Lời giải
Phần diện tích giảm đi chính là diện tích hình bình hành có cạnh đáy là và chiều cao là chiều cao mảnh đất hình bình hành ban đầu.
Chiều cao hình bình hành là: 
Diện tích hình bình hành đó là:
Bài tập tự luyện
Bài 9. Tính diện tích hình bình hành, biết độ dài đáy là , chiều cao là .
Hướng dẫn giải 
Đổi về cùng đơn vị đo rồi tính
Áp dụng công thức tính diện tích hình bình hành ta có: 
Bài 10. Tính diện tích hình bình hành biết độ dài đáy là , chiều cao bằng nửa độ dài đáy.
Hướng dẫn giải 
Áp dụng công thức tính diện tích hình bình hành ta có: 
Bài 11. Tính diện tích hình bình hành, biết tổng số đo độ dài đáy và và chiều cao là , độ dài đáy hơn chiều cao .
Hướng dẫn giải 
Độ dài đáy của hình bình hành là 
Chiều cao cua hình bình hành là 
Diện tích của hình bình hành là 
Bài 12.  Một hình bình hành có diện tích bằng , độ dài đáy là . Tính chiều cao của hình bình hành đó.
Hướng dẫn giải
Chiều cao của hình bình hành (cm)
Bài 13. Một hình bình hành có diện tích bằng , độ dài đáy bằng . Tính chiều cao của hình bình hành đó.
Hướng dẫn giải 
Diện tích 
Chiều cao của hình bình hành (dm)
Bài 14.  Một hình bình hành có diện tích bằng diện tích hình vuông cạnh , chiều cao bằng . Tính độ dài đáy của hình đó.
Hướng dẫn giải 
Diện tích hình bình hành là 
Dộ dài đáy của hình bình hành là 
Bài 15. Một mảnh vườn hình bình hành có độ dài đáy bằng , chiều cao bằng . Trên mảnh vườn đó người ta trồng các cây bưởi. Cứ trồng 1 cây bưởi. Hỏi cả mảnh vườn đó trồng được bao nhiêu cây bưởi?
Hướng dẫn giải
Diện tích mảnh vườn: 
Mảnh vườn trồng được cây bưởi là cây
B. Hình thoi
Dạng 1. Nhận biết hình thoi
I. Phương pháp giải.
Các dấu hiệu nhận biết hình thoi:
	1. Tứ giác có bốn cạnh bằng nhau là hình thoi
	2. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
	3. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
	4. Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
II.Bài toán.
Bài 1. Giải thích vì sao các hình vẽ dưới đây là hình thoi.
Lời giải
Các tứ giác ở hình 102a, b, c, e là hình thoi.
- Hình 102a: là hình thoi (theo dấu hiệu nhận biết số 1)
- Hình 102b: là hình thoi (theo dấu hiệu nhận biết 4)
- Hình 102c: là hình thoi (t
heo dấu hiệu nhận biết 3)
Dạng 2. Cách vẽ hình thoi	
I. Phương pháp giải.
	Dựa vào các tính chất của hình thoi để vẽ hình bình thoi.
II. Bài toán.
Bài 1. Vẽ hình thoi có cạnh bằng .
Lời giải
Bước 1. Vẽ đoạn thẳng . 
Bước 2. Vẽ đường thẳng đi qua B. Lấy điểm C trên đường thẳng đó sao cho . 
Bước 3. Vẽ đường thẳng đi qua C và song song với cạnh AB. Vẽ đường thẳng đi qua A và song song với cạnh BC.
Bước 4. Hai đường thẳng này cắt nhau tại D, ta được hình thoi ABCD.
Bài 2. Vẽ hình thoi ABCD biết và .
Lời giải
Bước 1. Dùng thước vẽ đoạn thẳng .
Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính .
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính , phần đường tròn này cắt phần đường tròn tâm A ở bước 2 tại hai điểm B và D.
Bước 4. Dùng thước vẽ các đoạn thẳng BA, BC, DA, DC. Ta được hình thoi ABCD.
Bài 3. Vẽ hình thoi có cạnh bằng 5 cm.
Lời giải
Cách vẽ tương tự bài 1
Bài 4. Vẽ bằng thước và compa hình thoi EFGH có cạnh EF = 6 cm; EG = 9 cm.
Lời giải
Cách vẽ tương tự bài 2
Dạng 3. Tính chu vi và diện tích hình thoi
I. Phương pháp giải.
	Dựa vào công thức tính chu vi và diện tích hình thoi; mối quan hệ giữa các cạnh của hình thoi.
II. Bài toán.
Bài 1. Tính diện tích hình thoi, biết:
a) Độ dài các đường chéo là và .
b) Độ dài các đường chéo là và .
Lời giải
a)Diện tích của hình thoi là: .
b) Đổi 4m = 40dm.
Diện tích của hình thoi là: .
Bài 2: Tính diện tích hình thoi biết là hình vuông và hai đường chéo của hình vuông ( là điểm chính giữa AO; N là điểm chính giữa OC)
Lời giải
Hai đường chéo hình vuông bằng nhau và cắt nhau tại trung điểm mỗi đường nên
Vì điểm M, N là các điểm chính giữa của OA, OC nên:
Do đó hình thoi có độ dài đường chéo 
Đường chéo 
Diện tích hình thoi là
Bài 3. Một miếng bìa hình bình hành có chu vi bằng 2m. Nếu bớt chiều dài đi 2dm thì ta được miếng bìa hình thoi có diện tích 6dm2. Tìm diện tích miếng bài hình bình hành đó. 
Lời giải
 là hình thoi nên 
là hình bình hành nên 
Chu vi hình bình hành là: 
Gọi h là độ dài đường cao của hình thoi AMND kẻ từ điểm M xuống cạnh DN
h đồng thời là độ dài đường cao của hình bình hành ABCD
Diện tích hình bình hành là:
Bài 4. Một mảnh vườn hình thoi có tổng độ dài hai đường chéo là , biết đường chéo thứ nhất bằng độ dài đường chéo thứ hai
a) Tính diện tích mảnh vườn đó.
b) Người ta dành diện tích mảnh vườn để làm nhà ở và vườn hoa. Tính diện tích để làm nhà ở và vườn hoa.
Lời giải
a) Độ dài đường chéo lớn là 
Độ dài đường chéo nhỏ là 
Diện tích mảnh vườn là 
b) Diện tích để làm nhà ở và vườn hoa là
Bài 5. Một mảnh vườn hình thoi có tổng hai đường chéo bằng , đường chéo thứ nhất hơn đường chéo thứ hai.
a) Tìm độ dài mỗi đường chéo.
b) Tính diện tích mảnh vườn.
c) Trên mảnh đất người ta dành 25% diện tích đất để trồng rau 46,5% diện tích để trồng ngô hỏi diện tích còn lại chiếm bao nhiêu diện tích mảnh vườn?
Lời giải
a) Đường chéo thứ hai của mảnh vườn là 
Đường chéo thứ nhất của mảnh vườn là 
b) Diện tích mảnh vườn là 
c) Số phần trăm diện tích còn lại của mảnh vườn là
Bài 6. Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình 153. Hãy tính diện tích phần con đường EBGF (EF//BG) và diện tích phần còn lại của đám đất.
Lời giải
Con đường hình bình hành EBGF có diện tích: 
Đám đất hình chữ nhật ABCD có diện tích: 
Diện tích phần còn lại của đám đất:
Bài tập tự luyện:
Bài 7. Tính diện tích hình thoi có cạnh bằng , tổng hai đường chéo bằng .
Hướng dẫn giải
Độ dài đường chéo bé là .
Độ dài đường chéo lớn là .
Diện tích vườn hoa hình thoi là .
Bài 8. Tính cạnh của hình thoi có diện tích bằng , tổng hai đường chéo bằng .
Hướng dẫn giải
Độ dài đường chéo bé là .
Độ dài đường chéo lớn là .
Diện tích thửa ruộng hình thoi là .
Bài 9. Một mảnh vườn hình thoi có tổng độ dài hai đường chéo . Tính diện tích mảnh vườn hình thoi; biết rằng đường chéo thứ nhất bằng một nửa độ  dài đường chéo thứ hai.
Hướng dẫn giải
Vì đường chéo thứ nhất bằng một nửa đường chéo thứ hai hay đường chéo thứ hai gấp đôi đường chéo thứ nhất.
Tổng số phần bằng nhau là (phần).
Độ dài đường chéo thứ nhất là .
Độ dài đường chéo thứ hai là .
Diện tích mảnh vườn hình thoi là 
Bài 10. Một mảnh đất hình thoi có đường chéo thứ nhất là . Độ dài đường chéo thứ hai bằng đường chéo thứ nhất. Người ta sử dụng diện tích mảnh đất ấy để trồng hoa.Tính diện tích trồng hoa.
Hướng dẫn giải
Độ dài đường chéo thứ hai là .
Diện tích mảnh đất hình thoi là .
Diện tích trồng hoa là .
Bài 11. Một hình thoi có độ dài đường chéo thứ nhất bằng cạnh hình vuông có chu vi . Tính diện tích hình thoi đó, biết tổng độ dài hai đường chéo là .
Hướng dẫn giải
Cạnh của hình vuông là .
Đường chéo thứ nhất có độ dài bằng cạnh của hình vuông nên bằng .
Độ dài đường chéo thứ hai là . 
Diện tích hình thoi là .
Bài 12. Một mảnh vườn hình thoi có độ dài hai hai đường chéo là và . Ở giữa vườn người ta xây một bể cá hình tròn bán kính phần còn lại để trồng hoa . Tính diện tích phần vườn trồng hoa.
Hướng dẫn giải
Diện tích mảnh vườn hình thoi là .
Diện tích bể cá hình tròn là .
Diện tích phần vườn trồng hoa là .
–HẾT—