Giáo án ôn tập Toán 8 (Cánh diều) - Chương 3, Bài 4: Đồ thị của hàm số bậc nhất y=ax+b (a≠0)
A. KIẾN THỨC TRỌNG TÂM
1. Đồ thị hàm số
Đồ thị hàm số :
Là một đường thẳng.
Cắt trục tung tại điểm có tung độ bằng b.
2. Cách vẽ đồ thị hàm số :
* Trường hợp1 : Xét hàm số .
Để vẽ đồ thị hàm số này ta cót hể xác định điểm A(1;a) rồi vẽ đường thẳng đi qua hai điểm O và A.
* Trường hợp2 : Xét hàm số :
Để vẽ đồ thị hàm số này ta có thể xác định hai điểm P(0;b) và Q rồi vẽ đường thẳng đi qua hai điểm đó.
3. Hệ số góc của đường thẳng
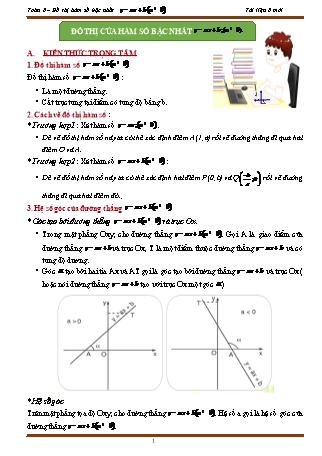
* Góc tạo bởi đường thẳng và trục Ox.
Trong mặt phẳng Oxy, cho đường thẳng . Gọi A là giao điểm của đường thẳng và trục Ox, T là một điểm thuộc đường thẳng và có tung độ dương.
Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng và trục Ox ( hoặc nói đường thẳng tạo với trục Ox một góc
Bạn đang xem tài liệu "Giáo án ôn tập Toán 8 (Cánh diều) - Chương 3, Bài 4: Đồ thị của hàm số bậc nhất y=ax+b (a≠0)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Giáo án ôn tập Toán 8 (Cánh diều) - Chương 3, Bài 4: Đồ thị của hàm số bậc nhất y=ax+b (a≠0)
ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT A. KIẾN THỨC TRỌNG TÂM 1. Đồ thị hàm số Đồ thị hàm số : Là một đường thẳng. Cắt trục tung tại điểm có tung độ bằng b. 2. Cách vẽ đồ thị hàm số : * Trường hợp1 : Xét hàm số . Để vẽ đồ thị hàm số này ta cót hể xác định điểm A(1;a) rồi vẽ đường thẳng đi qua hai điểm O và A. * Trường hợp2 : Xét hàm số : Để vẽ đồ thị hàm số này ta có thể xác định hai điểm P(0;b) và Q rồi vẽ đường thẳng đi qua hai điểm đó.. 3. Hệ số góc của đường thẳng * Góc tạo bởi đường thẳng và trục Ox. Trong mặt phẳng Oxy, cho đường thẳng . Gọi A là giao điểm của đường thẳng và trục Ox, T là một điểm thuộc đường thẳng và có tung độ dương. Góc tạo bởi hai tia Ax và AT gọi là góc tạo bởi đường thẳng và trục Ox ( hoặc nói đường thẳng tạo với trục Ox một góc ) * Hệ số góc. Trên mặt phẳng tọa độ Oxy, cho đường thẳng . Hệ số a gọi là hệ số góc của đường thẳng . * Vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy. Cho hai đường thẳng d: và d’ : . Nếu d song song với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d song song với d’. Nếu d trùng với d’ thì a = a’, b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’. Nếu d và d’ cắt nahu thì a a’ thì d cắt d’. B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI Dạng 1: Vẽ đồ thị hàm số Nếu ta có đường thẳng đi qua hai điểm . Nếu đường thẳng đi qua hai điểm . Ví dụ 1. Vẽ đồ thị của các hàm số sau: a) ; b) ; c) . Lời giải a/ . Nếu x = 1 thì y = 2, ta được A(1;2) thuộc đồ thị hàm số . Vậy đồ thi của hàm số là đường thẳng đi qua hai điểm O(0;0) và A(1;2). b/ BGT x 0 1 y 1 3 Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;1); B(1;3) c/ BGT x 0 1 y -2 -3 Vậy đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-2); B(1;-3) Ví dụ 2. Vẽ đồ thị các hàm số sau trong cùng một hệ trục tọa độ: ; ; . Lời giải * BGT x 0 1 y -4 -2 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-4); B(1;-2) * BGT x 0 1 y 3 6 Đồ thị của hàm số là đường thẳng đi qua hai điểm C(0;3); D(1;6) * Nếu x = 1 thì y = -1, ta được E(1;-1) thuộc đồ thị hàm số . Vậy đồ thi của hàm số là đường thẳng đi qua hai điểm O(0;0) và E(1;-1). Ví dụ 3. a) Vẽ đồ thị của các hàm số và trong cùng một mặt phẳng tọa độ. b) Gọi , lần lượt là giao điểm của đường thẳng ; với trục hoành và giao điểm của hai đường thẳng là . Tìm tọa độ giao điểm , , . Lời giải a/ Đồ thị của các hàm số và . BGT: x 0 -3 y 2 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;2); B(-3;0) BGT: x 0 -1 y 2 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;2); C(-1;0) b/ Dựa vào đồ thị hàm số trên ta có : Giao điểm của đường thẳng với trục hoành là A (-3;0). Giao điểm của đường thẳng với trục hoành là B (-1;0) Giao điểm của hai đường thẳng và là C (0;2) Dạng 2: Hệ số góc của đường thẳng Trên mặt phẳng tọa độ Oxy, cho đường thẳng . Hệ số a gọi là hệ số góc của đường thẳng . Ví dụ 4. Cho đường thẳng (d) : a/ Vẽ đường thẳng (d) trong mặt phẳng tọa độ . b/ Tìm hệ số góc của đường thẳng (d). Lời giải. a/ BGT: x 0 1 y -2 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-2); B(1;0) b/ Hệ số góc của đường thẳng : là 2. Ví dụ 5. Xác định đường thẳng đi qua điểm M(1;2) có hệ số góc bằng 3. Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ. Lời giải. Vì đường thẳng có hệ số góc bằng 3 nên a = 3. Khi đó d có dạng : Mà d đi qua M(1;2) nên thay x = 1; y = 2 vào d ta được : + b = 2 hay b = -1 Vậy đường thẳng d có dạng : Vẽ đường thẳng d : trên mặt phẳng tọa độ Oxy. BGT: x 0 1 y -1 2 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-1); B(1;2) Dạng 3: Xét vị trí tương đối của hai đường thẳng trong mặt phẳng tọa độ Oxy Cho hai đường thẳng d: và d’ : . Nếu d song song với d’ thì a = a’; b = b’. Ngược lại, nếu a = a’; b = b’ thì d song song với d’. Nếu d trùng với d’ thì a = a’, b = b’. Ngược lại, nếu a = a’; b = b’ thì d trùng với d’. Nếu d và d’ cắt nahu thì a a’ thì d cắt d’. Ví dụ 5. Cho hàm số : . a/ Xác định a, biết đồ thị hàm số song song với đường thẳng b/Vẽ đồ thị hàm số tìm được ở câu a. Tính diện tích tam giác được tạo bởi đồ thị hàm số và các trục tọa độ. Lời giải. a/ Vì đồ thị hàm số song song với đường thẳng y = -x nên a = -1. Vậy, hàm số có dạng : b/ Vẽ đồ thị hàm số : . Ta lấy hai điểm A(0;2) và B(2;0). Nối A và B ta có đồ thị cần vẽ : c/ Diện tích tam giác OAB là : (đvdt). Ví dụ 6. Cho hai đường thẳng : . a/ Chứng tỏ rằng hai đường thẳng cắt nhau. b/ Vẽ hai đường thẳng này trên cùng một hệ trục tọa độ. Từ đó xác định tọa độ giao điểm A của hai đường thẳng đó. c/ Xác định đường thẳng (d) :đi qua A và song song với đường thẳng d/ Xác định đường thẳng (d’) :đi qua A và song song với đường thẳng Lời giải. a/ Hai đường thẳng có hệ số góc khác nhau nên hai đường thẳng đó cắt nhau. b/ Vẽ hai đường thẳng trên cùng một hệ trục tọa độ. Đồ thị của hàm số y = 2x +1 là đường thẳng đi qua hai điểm A(0;1); B(1;3) Đồ thị của hàm số y = x + 1 là đường thẳng đi qua hai điểm A(0;1); C(1;2) Tọa độ giao điểm A của hai đường thẳng : Dựa vào đồ thị hàm số trên giao điểm của hai đường thẳng là A(0;1). c/ Đường thẳng (d) song song với đường thẳng y = -4x + 1 nên a = -4 Đường thẳng (d) có dạng y = -4x + b; Vì (d) đi qua A (0;1) nên thay x = 0; y = 1 vào (d) ta được : (-4).0 + b = 1 hay b = 1 Vậy đường thẳng (d) có dạng y = -4x + 1. d/ Đường thẳng (d’) song song với đường thẳng nên a = Đường thẳng (d’) có dạng y = x + b; Vì (d’) đi qua A (0;1) nên thay x = 0; y = 1 vào (d’) ta được : .0 + b = 1 hay b = 1 Vậy đường thẳng (d’) có dạng y = x + 1. C. BÀI TẬP VẬN DỤNG Bài 1. Vẽ đồ thị của các hàm số sau: a); b) ; c) . Lời giải: a/ Đồ thi của hàm số là đường thẳng đi qua hai điểm O(0;0) và A(1;3). b/ BGT: x 0 1 y -1 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-1); B(1;0) c/ . BGT: x 0 1 y -2 -5 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-2); B(1;-5) Bài 2. Xác định hệ số góc của các đường thẳng sau : Lời giải: Hệ số góc của đường thẳng (d) là -3. Hệ số góc của đường thẳng (d’) là 4. Hệ số góc của đường thẳng (d’’) là . Hệ số góc của đường thẳng (d’’’) là -0,4. Bài 3. Vẽ đồ thị của các hàm số và trong cùng một mặt phẳng tọa độ. Lời giải: Đồ thị của các hàm số và trong cùng một mặt phẳng tọa độ. BGT: x 0 1 y -6 -3 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;-6); B(1;-3) BGT: x 0 1 y 2 4 Đồ thị của hàm số là đường thẳng đi qua hai điểm C(0;2); D(1;4) Bài 4. a) Vẽ đồ thị của các hàm số và trong cùng một mặt phẳng tọa độ. b) Gọi , lần lượt là giao điểm của đường thẳng . với trục tung và giao điểm của hai đường thẳng là . Tìm tọa độ giao điểm , , . c) Tính diện tích tam giác . Lời giải: a/ Đồ thị của các hàm số và trong cùng một mặt phẳng tọa độ. BGT: x 0 4 y 4 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm A(0;4); C(4;0) BGT: x 0 4 y -4 0 Đồ thị của hàm số là đường thẳng đi qua hai điểm B(0;-4); C(4;0) b/ Dựa vào đồ thị hàm số trên ta có : Giao điểm của đường thẳng với trục tung là A (0;4). Giao điểm của đường thẳng với trục tung là B (0;-4) Giao điểm của hai đường thẳng và là C (4;0) c/ Diện tích tam giác ABC là : OC = 4 ; AB = 8 (đvdt). Bài 5. Cho hàm số bậc nhất y = ax + 1. a/ Xác định hệ số góc a, biết rằng đồ thị hàm số đi qua điểm A(-1;0,5). b/ Vẽ đồ thị hàm số với giá trị a tìm được trong câu trên. Lời giải: a/ Vì đồ thị hàm số đi qua A(-1;0,5) . Thay x = -1 và y = 0,5 vào y = ax + 1 ta được : a.(-1) + 1 = 0,5 1 – a = 0,5 a = 1 – 0,5 = 0,5 Vậy hệ số góc a = 0,5. b/ Vẽ đồ thị hàm số y = 0,5x + 1 BGT: x 0 2 y 1 2 Đồ thị của hàm số y = 0,5x + 1 là đường thẳng đi qua hai điểm A(0;1); B(2;2). Bài 6. Cho hàm số với là tham số. a) Tìm để đồ thị hàm số đi qua điểm . b) Tìm để đồ thị hàm số đi qua điểm . c) Vẽ đồ thị hàm số tìm được ứng với giá trị của tìm được ở câu a) và b) trên cùng mặt phẳng tọa độ . Lời giải: a/ Vì đồ thị hàm số đi qua điểm A(1;2) nên thay x = 1 ; y = 2 vào hàm số ta được : (2m – 1).1 + 1 = 2 2m – 1 + 1 = 2 2m = 2 m = 1 Vậy m = 1 đồ thị hàm số đi qua điểm A(1;2). b/ Vì đồ thị hàm số đi qua điểm B(3;-2) nên thay x = 3 ; y = -2 vào hàm số ta được : (2m – 1).3 + 1 = -2 2m – 3 + 1 = -2 2m - 3 = -3 2m = 0 m = 0 Vậy m = 0 đồ thị hàm số đi qua điểm B(3;-2). c/ Với m = 1 thì y = x + 1 m = 0 thì y = -x + 1. Đồ thị của hàm số y = x + 1 là đường thẳng đi qua hai điểm A(0;1); B(-1;0). Đồ thị của hàm số y = -x + 1 là đường thẳng đi qua hai điểm A(0;1); C(1;0). Bài 7. Một người đi bộ chuyển động đều trên đường thẳng với vận tốc 3 km/h. Gọi s (m) là quãng đường đi được trong t (giờ). a/ Lập công thức tính s quãng đường đi được theo thời gian t. b/ Vẽ đồ thị của hàm số ở câu a theo biến số t. Lời giải: a/ Quãng đường đi được theo thời gian t là : S = v.t = 3t (m). b/ Đồ thị của hàm số s = 3t là đường thẳng đi qua hai điểm O(0;0); A(1;3). Bài 8. Hãng taxi thứ nhất có giá như sau : mở cửa là 10 nghìn đồng, sau đó mỗi km giá 12 nghìn đồng. Hãng taxi thứ hai có giá như sau : Mỗi km tính giá 14 nghìn đồng. a/ Viết công thức tính y (số tiền khách phải trả) theo x (số km xe chở khách) của mỗi hãng xe taxi. b/ Xét vị trí tương đối của hai đường thẳng vừa tìm ở câu a. Lời giải: a/ Công thức tính số tiền phải trả của hãng xe taxi thứ nhất : y = 12x + 10; của hãng xe taxi thứ hai : y = 14x. b/ Xét vị trí tương đối của hai đường thẳng y = 12x + 10; y = 14x. Hai đường thẳng y = 12x + 10; y = 14x có hệ số góc khác nhau ( 12 14) nên hai đường thẳng đó cắt nhau. Bài 9. Cho hai đường thẳng và . a) Vẽ các đường thẳng , trong cùng một hệ trục tọa độ; b) Dựa vào đồ thị, hãy tìm tọa độ giao điểm của và . ĐS: (. Bài 10. Cho hai đường thẳng và . a) Vẽ các đường thẳng , trong cùng một hệ trục tọa độ; b) Dựa vào đồ thị, hãy tìm tọa độ giao điểm của và . ĐS: . Bài 11. Cho ba đường thẳng , và . a) Vẽ các đường thẳng , trong cùng một hệ trục tọa độ; b) Dựa vào đồ thị, hãy tìm tọa độ giao điểm của và . Bài 12. Cho ba đường thẳng , và . a) Vẽ các đường thẳng , trong cùng một hệ trục tọa độ; b) Tìm giao điểm của hai đường thẳng và ; ĐS: . c) Tìm giá trị của tham số để đường thẳng đi qua điểm ; ĐS: . Bài 13. Cho ba đường thẳng , và . Tìm giá trị của để hai đường thẳng cắt tại một điểm thuộc đường thẳng . ĐS: . Bài 14. Chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong số các đường thẳng sau : ; ; ; ; Bài 15. a/ Xác định đường thẳng (d) :đi qua A(1;5) và song song với đường thẳng b/ Vẽ đường thẳng vừa tìm ở câu a trên mặt phẳng tọa độ Oxy. Bài 16. Cho các đường thẳng : (d) : ; (d’) : ; (d’’) : . a/ Xét vị trí tương đối của các đường thẳng trên. b/ Xác định đường thẳng (d) :đi qua A(-2;2) và song song với đường thẳng (d’). Bài 17. Cho hai đường thẳng a/ Vẽ các đường thẳng , trong cùng một hệ trục tọa độ; b/ cắt Ox tại A, cắt Oy tại B. cắt Ox tại C, cắt Oy tại D. cắt tại M. Chứng minh tam giác MAC vuông tại A. c/ Tính diện tích tam giác MAC. Bài 18. Giá bán 1 kg măng cụt là 70 000 đồng. a/ Viết công thức biểu thị số tiền y(đồng) thu được khi bán x (kg) măng cụt. b/ Xác định hệ số góc của y . Lời giải: a/ Công thức biểu thị số tiền y (đồng) thu được khi bán x (kg) măng cụt là : y = 70 000x. b/ Hệ số góc của y là 70 000. Bài 19 Cho hàm số . a/ Xác định giá trị của a để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2. b/ Xác định giá trị của a để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3. c/ Vẽ đồ thị của hai hàm số ứng với giá trị a tìm được ở câu a và b trên cùng hệ trục tọa độ Oxy. Từ đó tìm giao điểm của hai đường thẳng vừa vẽ được. Lời giải: a/ Vì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2 khi đó x = 0; y = 2 Thay x = 0; y = 2 vào đồ thị hàm số ta được : (a -1).0 + a = 2 a = 2 Vậy a = 2. b/ Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3 khi đó x = -3 ; y = 0 Thay x = -3; y = 0 vào đồ thị hàm số ta được : (a – 1).(-3) + a = 0 -3a + 3 + a = 0 -2a + 3 = 0 a = Vậy a = c/ Với a = 2 khi đó y = x + 2. a = khi đó y = x + 2 Đồ thị của hàm số y = x + 2 là đường thẳng đi qua hai điểm A(0;2); B(-2;0). Đồ thị của hàm số y = x + 2là đường thẳng đi qua hai điểm A(0;2); C(-4;0). Giao của hai đường thẳng trên là A (0;2). Bài 20. Cho hàm số a) Tìm để đồ thị hàm số đã cho cắt trục hoành tại điểm có hoành độ bằng . b) Tìm để đồ thị hàm số đã cho cắt trục tung tại điểm có tung độ bằng . Bài 21. Cho hàm số với là tham số. a) Tìm để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng , b) Tìm để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng Bài 20 và Bài 21 cách giải như trên.
File đính kèm:
 giao_an_on_tap_toan_8_canh_dieu_chuong_3_bai_4_do_thi_cua_ha.docx
giao_an_on_tap_toan_8_canh_dieu_chuong_3_bai_4_do_thi_cua_ha.docx

